Kurs MUI - część 13
Coś pożytecznego
W miarę postępów w uczeniu się MUI potrafimy pisać już coraz bardziej praktyczne programy. Z własnego doświadczenia wiem, że przy zdobywaniu nowej wiedzy chce się ją jak najszybciej zastosować w praktyce pisząc jakiś konkretny program, zamiast tłuc nikomu niepotrzebne ćwiczebne przykłady. Dlatego dziś napiszemy konkretną i niewątpliwie pożyteczną klasę, przyswajając przy okazji kolejną dawkę wiedzy. W ciągu kilku kolejnych odcinków napiszemy klasę będącą edytorem sampli muzycznych. Oczywiście na Amigę jest szereg programów do tego służących ale żaden nie korzysta z MUI, wspólnie będziemy mogli wypełnić tę lukę. Zanim jednak rzucicie się do klawiatur warto poczynić wstępne założenia na temat projektowanej klasy.
Pierwsze pytanie - jaki format sampla przyjmiemy? Niewątpliwie 16-bitowy - trzeba iść z postępem. Najczęściej stosuje się liczby ze znakiem, zatem nasz sampel będzie tablicą liczb typu WORD. Klasa będzie miała za zadanie wyświetlić wybrany fragment sampla w postaci wykresu. Będą nam potrzebne trzy atrybuty: adres tablicy, pierwszy element do wyświetlenia i ilość wyświetlanych elementów. Wydaje się to dość skromnym zestawem. Jednak trzeba tu wziąć pod uwagę sposób w jaki z klas buduje się program. Zaczynamy od najprostszej klasy, która po prostu wyświetli fragment pamięci interpretując dane jako liczby 16-bitowe ze znakiem. Następnie będziemy tworzyć z niej klasy podrzędne dodając po trochu nowe możliwości. Takie podejście ma szereg zalet. W każdej kolejnej klasie koncentrujemy się na małym, ściśle określonym zadaniu. Ułatwia to pisanie, testowanie i usuwanie błędów. Usiłowanie wciśnięcia wyświetlania sampla, obsługi myszki, clipboardu, suwaka do scrollowania, podawania współrzędnych czasowych i tak dalej, doprowadzi nas do klasy-monstrum z dużym i niewygodnym kodem źródłowym. Co gorsza, jeżeli będziemy chcieli napisać klasę do edycji sampli stereo, cały kod trzeba powtórzyć od nowa. W wariancie z szeregiem klas weźmiemy po prostu dwa proste obiekty wyświetlające, nadbudowa pozostanie prawie bez zmian.
Mamy więc przed sobą ściśle określone zadanie. Klasa będzie oczywiście wyprowadzona z klasy Area. Jakie metody należy napisać? Na pewno MUIM_Draw, niezbędna też będzie MUIM_AskMinMax, OM_NEW oraz OM_SET (abyśmy mogli zmieniać wyświetlany fragment) i OM_GET (może się przydać później). Najpierw kilka słów o konstruktorze - nasza praca tutaj ogranicza się do odczytania wartości atrybutów i w razie ich braku ustawienia wartości domyślnych. Bardzo dobrze nadaje się do tego funkcja GetTagData() z utility.library. Mało że sama odnajduje tag w liście atrybutów, to automatycznie zwróci podaną wartość domyślną, jeżeli tag nie wystąpi w liście. Metodę MUIM_AskMinMax omówiłem dwa odcinki temu tutaj wykorzystałem - wspomnianą tylko wtedy - stałą MUI_MAXMAX. Dodając ją do pól MaxWidth i MaxHeight struktury MinMaxInfo określam maksymalne wymiary obiektu jako nieograniczone. Bliższe przyjrzenie się metodzie OM_GET ujawnia, że nie ma w niej nic nadzwyczajnego. W zależności od pobieranego atrybutu zapisuję zawartość odpowiedniego pola struktury danych obiektu pod adres podany w opg_Storage. Zwracam uwagę - jest to adres miejsca na dane, samo pole opg_Storage nie jest tym miejscem! Nie należy też zwracać wartości atrybutu na wyjściu funkcji, zwracamy po prostu TRUE, jeżeli rozpoznaliśmy atrybut, jeżeli nie, przekazujemy metodę klasie nadrzędnej.
 Nowością w metodzie OM_SET jest użycie znanej już nam funkcji
MUI_Redraw(). To oczywiste - po zmianie parametrów wykresu trzeba go
narysować od nowa. Inaczej jednak niż dwa odcinki temu podajemy znacznik
MADF_DRAWUPDATE, przez co MUI nie odrysuje tła ani ramki. Tło bowiem
rysujemy sobie sami, a odrysowanie ramki nie jest potrzebne - rozmiar
gadżetu nie zmienia się w danym momencie. I w ten sposób dochodzimy do
najbardziej rozbudowanej metody - MUIM_Draw. Myślę, że warto poświęcić
jej nieco uwagi. Na początku standardowo poprzez DoSuperMethodA()
pozwalamy MUI zrobić co jego. Następnie rysujemy tło - czarny prostokąt.
Oczywiście nic nie stoi na przeszkodzie abyście w ramach ćwiczeń dodali
do klasy atrybut pozwalający na zmianę koloru tła. Następnie, w
zależności od parametrów wykresu możemy się znaleźć w jednej z trzech
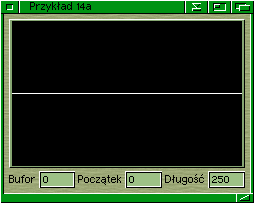
sytuacji. Po pierwsze bufora może w ogóle nie być (zerowy adres lub
zerowa długość). Wtedy rysujemy po prostu poziomą kreskę - "brak
sygnału". Nie można pominąć tej sytuacji - jej nieuwzględnienie skończy
się dzieleniem przez zero lub hitami Enforcera. My ją na szczęście
uwzględniliśmy, co widać na pierwszym rysunku.
Nowością w metodzie OM_SET jest użycie znanej już nam funkcji
MUI_Redraw(). To oczywiste - po zmianie parametrów wykresu trzeba go
narysować od nowa. Inaczej jednak niż dwa odcinki temu podajemy znacznik
MADF_DRAWUPDATE, przez co MUI nie odrysuje tła ani ramki. Tło bowiem
rysujemy sobie sami, a odrysowanie ramki nie jest potrzebne - rozmiar
gadżetu nie zmienia się w danym momencie. I w ten sposób dochodzimy do
najbardziej rozbudowanej metody - MUIM_Draw. Myślę, że warto poświęcić
jej nieco uwagi. Na początku standardowo poprzez DoSuperMethodA()
pozwalamy MUI zrobić co jego. Następnie rysujemy tło - czarny prostokąt.
Oczywiście nic nie stoi na przeszkodzie abyście w ramach ćwiczeń dodali
do klasy atrybut pozwalający na zmianę koloru tła. Następnie, w
zależności od parametrów wykresu możemy się znaleźć w jednej z trzech
sytuacji. Po pierwsze bufora może w ogóle nie być (zerowy adres lub
zerowa długość). Wtedy rysujemy po prostu poziomą kreskę - "brak
sygnału". Nie można pominąć tej sytuacji - jej nieuwzględnienie skończy
się dzieleniem przez zero lub hitami Enforcera. My ją na szczęście
uwzględniliśmy, co widać na pierwszym rysunku.
 Jeżeli jednak mamy co narysować, nadal stoją przed nami dwa alternatywne
podejścia do problemu. Pierwsze z nich stosuję, gdy próbek jest mniej
niż pikseli w obiekcie. Wtedy licznikiem pętli rysującej są próbki -
każda z nich zostanie narysowana. Ponieważ każda próbka zajmie co
najmniej jeden piksel, składa się z dwóch kresek: pionowej od
poprzedniej próbki i poziomej wyznaczającej poziom próbki. Z reguły
ilość pikseli nie podzieli się bez reszty przez ilość próbek. Aby w
miarę precyzyjnie odwzorować sampla, szerokość próbki zapisana jest jako
pomnożona przez 65536, można tę liczbę potraktować tak, że górne 16
bitów to część całkowita, a dolne - ułamkowa. Dzięki temu próbki są
rozłożone najdokładniej jak można - po prostu co któraś jest o 1 piksel
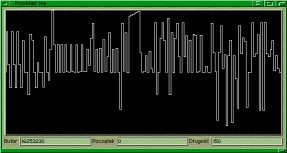
szersza. Ten wariant widzimy na rysunku. Na 549 pikseli przypada 150
próbek.
Jeżeli jednak mamy co narysować, nadal stoją przed nami dwa alternatywne
podejścia do problemu. Pierwsze z nich stosuję, gdy próbek jest mniej
niż pikseli w obiekcie. Wtedy licznikiem pętli rysującej są próbki -
każda z nich zostanie narysowana. Ponieważ każda próbka zajmie co
najmniej jeden piksel, składa się z dwóch kresek: pionowej od
poprzedniej próbki i poziomej wyznaczającej poziom próbki. Z reguły
ilość pikseli nie podzieli się bez reszty przez ilość próbek. Aby w
miarę precyzyjnie odwzorować sampla, szerokość próbki zapisana jest jako
pomnożona przez 65536, można tę liczbę potraktować tak, że górne 16
bitów to część całkowita, a dolne - ułamkowa. Dzięki temu próbki są
rozłożone najdokładniej jak można - po prostu co któraś jest o 1 piksel
szersza. Ten wariant widzimy na rysunku. Na 549 pikseli przypada 150
próbek.
 Podobne podejście możnaby zastosować w przypadku gdy próbek jest więcej
niż pikseli. Szerokość próbki byłaby ułamkowa i niektóre po prostu
rysowalibyśmy jedna na drugiej. Tyle że sampel z powodzeniem może mieć
kilka milionów próbek (przeciętny utwór muzyczny np. ze zdekodowanego
pliku MP3 ma 30 - 70 MB). Jak długo będzie trwało rysowanie 5 milionów
kresek? Nawet na karcie graficznej za długo. Dlatego w tym przypadku
licznikiem pętli rysującej są piksele wykresu. Nawet przy setkach
megabajtów danych postawimy tylko kilkaset kresek. To przeżyją z
powodzeniem nawet kości AGA. I znowu stajemy przed problemem - trzeba
wybrać próbki do narysowania i powinny one być wybrane równomiernie. A
tak jak poprzednio z reguły liczba próbek nie podzieli się nam bez
reszty przez liczbę pikseli. Co gorsza nie możemy zastosować skalowania
- skok między kolejnymi rysowanymi próbkami może nam się nie zmieścić w
16, a nawet 24 bitach. Co robić? Arytmetyka 64-bitowa? Liczby
zmiennoprzecinkowe? Niekoniecznie, jest bardzo proste wyjście,
skorzystamy mianowicie z ułamków zwykłych (!). Przykładowo mamy 50
pikseli i 160 próbek. Będziemy więc rysować co trzecią próbkę, ale
czasem co czwartą. Dzielimy sobie 160 / 50 = 3 r 10 (podstawówka się
przypomina...) co oznacza ni mniej ni więcej jak 3 i 10/50. Ponieważ
mianownik ułamka jest z góry znany, wystarczy pamiętać licznik. W naszym
kodzie odstęp między próbkami pamiętany jest w 'step' (część całkowita)
i 'remd' (licznik ułamka), aktualny numer próbki odpowiednio w
'sample_number' i 'remdacc'. W pętli dodajemy do aktualnej pozycji za
każdym razem część całkowitą i ułamkową. W momencie gdy licznik stanie
się większy od mianownika po prostu... wyłączamy całkowitą jedynkę i
przerzucamy ją do części całkowitej (instrukcja if)! Proste, szybkie i
skuteczne. Oczywiście tablicę próbek indeksujemy tylko częścią
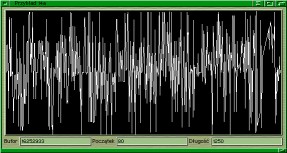
całkowitą... Efekty widać na rysunku powyżej. Tym razem na 549 pikseli mamy
1250 próbek rysujemy więc mniej więcej co drugą. Na obu rysunkach
widzimy początek pamięci ROM (KickStartu) w okolicach adresu $00F80000.
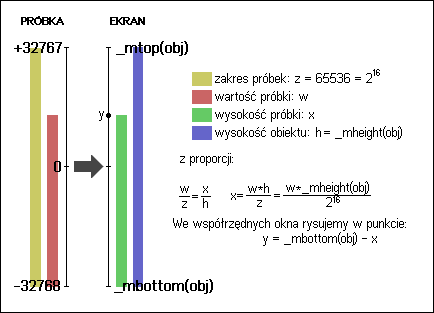
Pozostało nam omówienie skalowania sampla w pionie. Tu najlepiej
sprawdzi się metoda rysunkowa, która wyjaśni dość skomplikowane
wyrażenie z kodu źródłowego (rysunek poniżej). Skalowanie jak zwykle opiera
się na proporcji, do tego dochodzi odpowiednie przesunięcie skali.
Podobne podejście możnaby zastosować w przypadku gdy próbek jest więcej
niż pikseli. Szerokość próbki byłaby ułamkowa i niektóre po prostu
rysowalibyśmy jedna na drugiej. Tyle że sampel z powodzeniem może mieć
kilka milionów próbek (przeciętny utwór muzyczny np. ze zdekodowanego
pliku MP3 ma 30 - 70 MB). Jak długo będzie trwało rysowanie 5 milionów
kresek? Nawet na karcie graficznej za długo. Dlatego w tym przypadku
licznikiem pętli rysującej są piksele wykresu. Nawet przy setkach
megabajtów danych postawimy tylko kilkaset kresek. To przeżyją z
powodzeniem nawet kości AGA. I znowu stajemy przed problemem - trzeba
wybrać próbki do narysowania i powinny one być wybrane równomiernie. A
tak jak poprzednio z reguły liczba próbek nie podzieli się nam bez
reszty przez liczbę pikseli. Co gorsza nie możemy zastosować skalowania
- skok między kolejnymi rysowanymi próbkami może nam się nie zmieścić w
16, a nawet 24 bitach. Co robić? Arytmetyka 64-bitowa? Liczby
zmiennoprzecinkowe? Niekoniecznie, jest bardzo proste wyjście,
skorzystamy mianowicie z ułamków zwykłych (!). Przykładowo mamy 50
pikseli i 160 próbek. Będziemy więc rysować co trzecią próbkę, ale
czasem co czwartą. Dzielimy sobie 160 / 50 = 3 r 10 (podstawówka się
przypomina...) co oznacza ni mniej ni więcej jak 3 i 10/50. Ponieważ
mianownik ułamka jest z góry znany, wystarczy pamiętać licznik. W naszym
kodzie odstęp między próbkami pamiętany jest w 'step' (część całkowita)
i 'remd' (licznik ułamka), aktualny numer próbki odpowiednio w
'sample_number' i 'remdacc'. W pętli dodajemy do aktualnej pozycji za
każdym razem część całkowitą i ułamkową. W momencie gdy licznik stanie
się większy od mianownika po prostu... wyłączamy całkowitą jedynkę i
przerzucamy ją do części całkowitej (instrukcja if)! Proste, szybkie i
skuteczne. Oczywiście tablicę próbek indeksujemy tylko częścią
całkowitą... Efekty widać na rysunku powyżej. Tym razem na 549 pikseli mamy
1250 próbek rysujemy więc mniej więcej co drugą. Na obu rysunkach
widzimy początek pamięci ROM (KickStartu) w okolicach adresu $00F80000.
Pozostało nam omówienie skalowania sampla w pionie. Tu najlepiej
sprawdzi się metoda rysunkowa, która wyjaśni dość skomplikowane
wyrażenie z kodu źródłowego (rysunek poniżej). Skalowanie jak zwykle opiera
się na proporcji, do tego dochodzi odpowiednie przesunięcie skali.
Gadżety na dole służą wyłącznie przetestowaniu klasy. Nie ulega bowiem wątpliwości, że docelowa klasa powinna być wyposażona w suwak i najlepiej jeszcze gadżety pozwalające wpisanie czasu sampla, a nie ilości próbek. Ale te dodatki dołączymy do klasy w następnych odcinkach. A tymczasem przyjrzyjmy się notyfikacjom aktualizującym parametry wykresu po wpisaniu wartości do gadżetów. Co tu robi ten hook (Update())? Dlaczego nie można zrobić notyfikacji bezpośrednio na parametr MUIA_String_Integer? To niestety jedna z niedoróbek MUI - mimo tego, że parametr może być pobrany ([G] w autodokach), notyfikacje nań ustawione nie działają... Dlatego niezbędne jest wywołanie hooka, który pobierze wartości liczbowe z gadżetów i ustawi atrybuty wykresów. Żeby zaś zmniejszyć rozmiary programu napisałem jeden hook z parametrem zamiast trzech oddzielnych.
To wszystko na dziś, zachęcam do przysyłania uwag i opinii o cyklu MUI na mój adres internetowy. Postaram się je uwzględnić w nadchodzących odcinkach. Na przykład poprzedni odcinek o ARexxie powstał w wyniku "zapotrzebowania społecznego". Dodatek - tutaj.


